Muesli LunarLander-v2 implementation - Loss설명

날짜:

개요

해당 글에서는 Muesli의 loss에 대해 추가적인 설명을 작성합니다.

먼저 뮤즐리는 뮤제로의 후속 연구로 많은 것을 뮤제로와 공유하는데, loss가 서로 다릅니다. 뮤제로는 self-play시에 action-selection을 위해서 수십~수백번의 MCTS실행을 통해서 search policy를 얻어내고 이에 따라 액션을 취합니다. (뮤즐리는 많은 알고리즘들과 유사하게 그냥 policy를 따라 액션을 선택합니다. 이 때문에 Self-play시에 훨씬 빠릅니다.) 그리고 뮤제로는 학습 시 self-play시에 얻었던 search policy를 unroll된 네트워크가 따라가게끔 둘의 차이를 cross entropy loss로 계산하는 loss를 사용합니다.

이러한 방법이 알파고 제로 때부터 뮤제로까지 효과적으로 쓰여왔는데, 한편으로는 이러한 방식이 다른 policy optimization식들과는 꽤나 다른 모습인 것을 많이들 의아해 했을 것 같습니다. 이러한 물음에서 시작된 것인지, "Monte-Carlo tree search as regularized policy optimization" 라는 논문에서 위에서 설명했던 MCTS를 사용해서 search policy를 찾고 loss를 구성하는 방법이 regularized policy optimization의 objective를 approximate하는 것으로 볼 수 있다는 설명을 내놓았습니다.

뮤즐리는 이러한 아이디어에 기반해 기존 뮤제로의 성능을 따라잡을 수 있는 regularized objective를 제시하였고, 이는 다음과 같습니다.

L_pg+cmpo

레귤라이저 옆의 람다는 하이퍼파라미터입니다. 레귤라이저에 들어가는 pi_cmpo는 다음과 같습니다.
pi_prior는 뮤즐리에서 업데이트되는 네트워크의 파라미터들을 exponential moving average로 저장하는 target network로부터 인퍼런스 되는 policy입니다. 그리고 advantage는 target network의 model(reward model, value model)들로부터 계산합니다. z_cmpo는 모든 action들에 대해서 pi_cmpo 분포를 구성할 때 valid 한 probability distribution임을 보장해주기 위해서 나눠주는 값(분자 계산값 모두 더한값)입니다. 

(Loss계산에서 사용되는 모든 advantage들은 normalized되어 사용이 되는데 이는 reward scale에 robust하기 위해 중요한 부분입니다. 이는 설명글에 설명되어 있습니다.)

위의 식을 직접 사용하는 것이 성능상 가장 좋지만 stochastic하게 식을 sample하는 방법도 소개가 됩니다. action space가 큰 경우에 모든 경우에 대해 전부 계산하지 않고 일부에 대해서만 계산하기 위함입니다.
Figure 6(b), KL식 직접 구하는 것과 sampling하는 것과 차이


첫번째 항(9번 식)은 아래의 식으로 샘플됩니다.
이는 trajectory에서 가져온 s,a에 대해서 importance weight를 구하고(policy_b는 behavior policy이며, importance weight는 [0,1]로 clip되어 사용됨), advantage는 괄호 안의 식으로 샘플되는데, G는 multi step return으로, 논문에서는 retrace estimator를 사용해서 구합니다. 

두번째 항(7번 식)은 아래의 식으로 샘플됩니다.
7번 식의 레귤라이저처럼 exact한 분포에 대해 KL을 취하는 대신 선택된 action들(이는 target network로부터 인퍼런스된 pi_prior에 따라 샘플됨)에 대해 각각 거리를 계산할 수 있는 구조로, 여기서의 z_cmpo는 아래의 식이 사용됩니다. z_init은 1이 사용됩니다. 
계산된 L_pg_cmpo는 첫번째 policy에 대한 loss로 사용이 됩니다.


L_m

그리고 미래 시점에 인퍼런스된 policy들에 대해서 model loss인 L_m이 사용되는데, 이는 input을 hidden state로 인코딩하는 인코더 역할을 하고 있는 representation network, dynamics network가 hidden state들의 표현을 학습하는데 도움이 되어 학습을 안정적으로 만들어 줍니다. 해당 식에 들어가는 pi_cmpo는 위의 그림에 그려둔 것과 같이 target network를 가지고 각 시점의 observation들로부터 one-step lookahead를 하여 계산합니다.
Figure 7(a), L_m 사용 성능 비교 (5-step, 1-step, 없는경우)


L_r, L_v

그리고 reward model들로 들어가는 L_r 및 value model들로 들어가는 L_v는 해당 시점에서 관찰된 reward와 value 값들을 학습합니다. 해당 값들은 스칼라 값 그대로 학습되는 것이 아니라 categorical reparametrization 기법을 통해서 학습이 됩니다. 이는 (설명글)에서 설명하였습니다.


이렇게 Regularized objective인 L_pg+cmpo, model loss인 L_m, value model과 reward model에 대한 loss L_v, L_r이 모두 합쳐져서 L_total = L_pg_cmpo + L_v/6/4 + L_r/5/1 + L_m의 형태로 들어가게 되고, 한번에 optimize됩니다. (각각 unroll된만큼 나눠지고, L_v의 경우 policy와 네트워크를 공유해서인지 loss를 더 낮춰주는 것이 안정적입니다.)




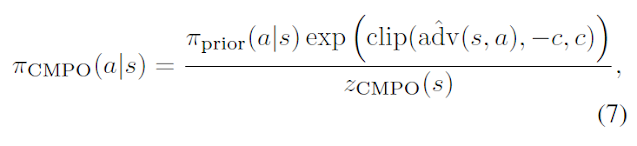
댓글

댓글 쓰기

가장 많이 본 글

이미지

구글 람다(LaMDA)란? - 구글의 언어 모델

 구글 람다(LaMDA)란? 구글 람다는 구글이 2021 Google I/O에서 발표한 언어 모델입니다. 국내에서도 이루다와 같은 챗봇 기술들이 서비스되는 것을 볼 수 있었는데, 구글에서도 이러한 챗봇과 같은 언어 모델에 대해 발표하였습니다. 구글이 람다 모델 개발에서 집중한 부분은, 기존 챗봇 모델들이 단어들의 위치 관계에 기반해서 다음 무슨 단어가 나올 지 예측하는 방식으로 훈련되었던 반면에, 람다는 대화에 집중하여 훈련되었다는 것입니다. 대화 모델 개발에 있어서 '말이 되는가'와 '질문에 대해 구체적인가' 둘 다 모두 중요합니다. 어떤 질문의 답변으로 "그거 좋네요!" 와 "잘 모르겠네요." 둘 다 답변으로 말이 되는 경우가 많습니다. 하지만 질문에 대해 구체적으로 연결된 정보를 내어주지는 못합니다. 구글은 구체적인 답변에 대해서도 잘 커버하는 것이 가능한 대화가 되게끔 학습을 시켰다고 합니다. 이러한 것은 영상에 나오는 예시에 보면 어떤 토픽에 대해 구체적으로 답변하는 모습을 볼 수 있습니다. 영상의 첫 예시에는 LaMDA가 사진의 행성인 명왕성이 되어 답변을 해 줍니다. (구글 CEO 순다 피차이의 LaMDA 시연 영상) 질문 :  내가 방문하면 어떤걸 볼 수 있는지 알려줘. LaMDA의 답변 : 너는 거대한 협곡들, 얼음들, 크레이터들을 볼 수 있어. 질문 : 그거 멋있네. LaMDA의 답변 :   이 여행은 분명 재미있을 꺼야. 엄청 추울 수 있으니까 코트를 들고 와. 질문 : 기억하고 있을께. 혹시 누가 방문했던 적 있어? LaMDA의 답변 : 응. 누군가 왔다 갔었지. 호라이즌스 우주선이 방문했었어. 질문 : 그때 정말 재미있었겠다. LaMDA의 답변 : 뉴 호라이즌스 팀이 날 보고 매우 좋아했어. 난 그들에게 그동안 가까이 볼 수 없었던 뒷편의 사진을 보내줬어. 종이비행기가 되어서 이야기 하는것도 신기합니다. 질문 : 좋은 종이비행기가 되는 비밀이 뭐야? LaMDA의 답변 : 글...
이미지

알파고 강화학습 원리

강화학습은 인공지능이 사용할 수 있는 최고의 정책을 찾아내는 방법입니다. 어떻게 행동하는게 가장 좋은 것인지 사람이 컴퓨터에게 직접 알려주지 않아도, 컴퓨터가 직접 시행착오를 겪으며 가장 좋은 정책을 찾아내는 것입니다. 강화학습에는 Agent(에이전트), State(상태), Action(행동), Reward(보상), Environment(환경), policy(정책)와 같은 개념들이 존재합니다. 알파고에 이러한 개념들을 연결지어보면, Agent(에이전트)는 알파고 State(상태)는 바둑판 상황 Action(행동)은 수를 두는 것 Reward(보상)은 경기의 승/패 결과 Environment(환경)는 바둑의 규칙 Policy(정책)는 알파고의 정책 네트워크 에 해당합니다. 인공지능이 행동을 할 때는 정책의 도움을 받습니다. 정책은 인공지능이 다음 행동을 선택할 때 어떤 행동이 좋을 지 추천을 해주는 역할을 합니다. 알파고의 정책 네트워크는 다음에 둘 수 있는 수들의 확률을 추천해줍니다. 높은 확률을 가진 수일수록 알파고는 판단과정에 더 큰 비중을 둡니다. (바둑판을 입력으로 넣으면 어디가 좋을지 확률을 알려준다) 알파고에서 강화학습을 진행할 때, 수많은 경기를 하며 시행착오를 겪습니다. 강화학습 알고리즘은 경기에서 얻은 시행착오를 기반으로 정책 네트워크가 알려주는 확률을 조정합니다. 조정된 확률은 다음 번 경기에 알파고가 더 똑똑하게 움직일 수 있게 해 줍니다. REINFORCE 알고리즘 알파고에서는 REINFORCE 알고리즘에 기반하여 시행착오와 정책 네트워크의 확률을 조정하는 과정을 진행합니다. 먼저  policy network(정책 네트워크)의 추천에 기반하여  승패가 확정되는 State인 Terminal State까지 자가대전을 진행합니다. 자가대전의 결과로 각 수를 두는 시점 time step t에 해당하는 State, Action, Reward를 얻게 됩니다. 이제 위에서 얻어낸  State, Action, Reward...
이미지

버텍스 AI란? - 구글 인공지능 플랫폼

버텍스 AI란?  버텍스 AI (Vertex AI)는 구글에서 제공하는 통합 머신러닝 플랫폼입니다. 구글 클라우드 플랫폼을 통해 제공됩니다. 머신러닝 모델을 직접 만들어 실제 비즈니스에 적용하는 것은 상당히 어려운 일입니다.  복잡한 신경망을 구성해야 하고, 데이터셋을 잘 준비해야 하며, 신경망을 학습시키기 위해 비싼 고성능 컴퓨터가 필요합니다. 머신러닝 모델을 만드는 것은 인공지능 전문 인력을 통해 많은 코드 작성이 필요합니다. 이는 비용이 크고 시간 또한 많이 걸리는 일입니다.  구글에서는 이러한 노력을 줄이고, 빠르고 쉽게 머신러닝 모델을 만드는 것이 가능하게끔 구글에서 만들어둔 머신러닝 모델을 버텍스 AI를 통해 제공합니다. 만들어진 모델 이외에 커스텀 모델이 필요하다면 커스텀할 수 있는 도구 또한 제공합니다. 경쟁사 플랫폼 대비 80%나 적은 코드 작성으로 커스텀이 가능합니다. https://codelabs.developers.google.com/codelabs/vertex-ai-custom-models   링크를 통해 실습을 지원합니다. 실습 내용 요약 구글 클라우드에서 실행되는 가상 머신을 Cloud Shell을 통해서 접근하여 작업이 가능합니다. Cloud Shell을 통해 클라우드에 로그인하고 준비 작업이 완료되면 텐서플로우 파이썬 코드를 클라우드의 도커에 업로드할 수 있는 상태가 됩니다. 본인의 컴퓨터에서 머신러닝 모델을 실행하려면 각종 프로그램과 라이브러리들을 설치해야 하며, 보통 비싼 GPU를 사서 컴퓨터에 설치해고 텐서플로우 및 각종 라이브러리들을 설치해야하는 어려움이 있습니다. 도커에는 이미 수많은 머신러닝, 데이터과학 프레임워크가 사전 설치되어 있기 때문에, 이러한 어려움을 겪지 않아도 됩니다. 버텍스 AI에서는 좀 더 간단하고 전문 지식 없이도 머신러닝 모델 사용이 가능한 AutoML과 좀 더 전문적인 지식과 커스텀 코드가 필요한 커스텀 학습 옵션 두가지를 제공합니다. 자신이 원하는 수준의...
이미지

카타고와 바둑 두어보기

바둑 인공지능 카타고와 바둑을 직접 두어볼 수 있는 사이트를 소개합니다. 카타고는  알파고와 완전 동일하지는 않으며 알파제로의 방법에 기반해 여러 기법을 추가해 만들어진 바둑 인공지능입니다. KataGui -  https://katagui.herokuapp.com/ [AI플레이] 버튼을 통해서 AI가 수를 두게 할 수 있고, 중간에 직접 두어볼 수도 있습니다. [베스트]를 누르면 그때그때 좋은 수들을 알려주고, 수들의 확률 분포를 바둑판 아래에 보여줍니다. 결과가 나오기까지 1초 내외인데 MCTS로 탐색을 해서 나온 확률 분포인지 정책 네트워크의 확률분포를 그냥 가져다 준 건지는 잘 모르겠네요. 아마 짧게라도 탐색을 해서 나온 분포가 아닐까 생각합니다. [스코어]를 누르면 현재 승리 가능성 (가치 네트워크의 출력값)을 바둑판 아래에 출력해주고, 대략적인 집수 계산을 해주는 것 같습니다. 중간에 딱 1수만 잘못 둬도 승률이 몇십 퍼센트씩 떨어지네요. 바둑 잘 두시는 분들은 정말 대단한 것 같습니다.
이미지

뉴럴 네트워크란?

인공지능 관련 글에는 항상 복잡하게 생긴 뉴럴 네트워크가 등장합니다.  뉴럴 네트워크는 인공지능 연구의 날개가 되어준 기술입니다. 예전에는 해결이 불가능했던 문제에 뉴럴 네트워크 기술을 적용하면 마법과 같은 결과물이 나오고는 합니다 . 뉴럴 네트워크는 사람의 신경 구조를 닮았다고 알려져 있습니다. 신경을 닮았기에  사람처럼 생각하는 힘을 가지게 된 걸까요?  마치 그럴 것 같지만 그렇지는  않습니다.  뉴럴 네트워크는 생각하는 특성보다는 기억을 잘 하는 특성을 가진 기술이며,  데이터 사이의 연관 관계를  기억 하는데에 사용됩니다. 조금 더 복잡하게 말하면 데이터 사이의 연관 관계를 나타내는 수식을 찾아내는데에 사용됩니다. 데이터 사이의 연관 관계 예를 들어 x=( 1,2,3,4,5)와 y=(2,4,6,8,10)의  데이터 묶음이 있습니다. 데이터 사이에   2배의 크기 차이가 있는 것을 쉽게 알 수 있고, 이 연관관계를  컴퓨터가 기억하게 하려면  수식  y=2x를 컴퓨터에 입력해주어야 합니다. (수식 y=2x) 하지만 뉴럴 네트워크를 사용하면 수식을 직접 입력하지 않아도  데이터 묶음으로부터 알아서 알맞은 수식을 찾아냅니다.  뉴럴 네트워크의 신경처럼 복잡하게 엮여있는 구조는 복잡한 수식을 표현할 수 있는 잠재력이 있습니다.  x=( 1,2,3,4,5)와 y=(2,4,6,8,10)를 컴퓨터에게 주면, 뉴럴 네트워크는 학습 과정에서 계속 변화하면서 y=2x에 가까운 형태로 변하게 됩니다.  이렇게 뉴럴 네트워크가 저절로 알맞은 수식의 형태로 변하는 능력은 데이터 묶음이 아주 복잡할때 큰 장점을 가집니다.  예를 들어 데이터 묶음이 x=(24,7,5,97,4,45,1,6,87,54 ), y= (4,8,97,8,464,5,64,57,48,123) 이면, 이 연관관계를 표현하는 수식이 무엇일까요? 이 관계를 표현하는...
이미지

블로그 글 목록

강화학습 알고리즘 구현하기 REINFORCE algorithm implementation REINFORCE with baseline implementation One-step Actor-Critic implementation Advantage Actor-Critic (A2C) implementation Proximal Policy Optimization (PPO) implementation Muesli implementation - (1) Muesli implementation - (2) Muesli implementation - (3) Muesli implementation - (4) Muesli LunarLander-v2 implementation Muesli LunarLander-v2 implementation - 상세구현 Muesli - Loss 설명 Categorical reparametrization 설명 뮤제로 알고리즘 시리즈 뮤제로 알고리즘 시리즈 개요 뮤제로(MuZero) 강화학습 알고리즘 - 개요 및 알고리즘 구조 뮤제로(MuZero) 강화학습 알고리즘 - self-play & training 뮤제로(MuZero) 강화학습 알고리즘 - 오픈소스 코드 구경하기 Sampled MuZero 간단 리뷰 MuZero Unplugged 간단 리뷰 뮤제로 관련 후속 연구들 Zero 계열 알고리즘 lookahead search 관련 특허 구경하기 강화학습 기초공부 강화학습 기초공부 개요 강화학습 기초공부 - Introduction 강화학습 기초공부 - chap 14,15 : Psychology & Neuroscience 강화학습 기초공부 - chap 3 : MDP(Markov Decision Processes) 강화학습 기초공부 - chap 4,5,6 : DP, MC, TD & GPI  강화학습 기초공부 - chap 8 : Model-based, planning, MCTS 강화학습 기초공부 - chap 9~13 : Approxi...
이미지

뉴럴 네트워크를 학습시키는 방법

앞서 작성한 글인  뉴럴 네트워크 개요 에서, 뉴럴 네트워크는 데이터 간의 연관관계를 기억하는 능력을 가지고 있고,  데이터로부터  연관관계를 표현할 수 있는  특정한 수식을 자동으로 찾아내는 물건이라 고 이야기 하였습니다. 어떻게 구성되어 있길래 특정 수식을 자동으로 찾아낼 수 있는 것일까요? 조금 바꾸어 말하면 뉴럴 네트워크는 어떻게 학습을 하는 것일까요? 간단한 뉴럴 네트워크 아래 그림은 간단한 형태의 뉴럴 네트워크입니다. 뉴럴 네트워크는 가장 왼쪽에 입력 데이터가 들어오면, 가장 오른쪽에 출력 데이터를 내보내 줍니다. 중간에는 많은 선들과 동그라미가 있습니다. 선 들은 각각 값을 가지고 있으며, 선은 자신의 왼쪽 동그라미의 값과 자신의 값을 곱하여 오른쪽 동그라미로 넘겨줍니다.  동그라미 는 들어오는 값을 모두 더하는 역할을 합니다. 그리고 더한 값이 0보다 크면 오른쪽으로 값을 내보내고, 0보다 작으면 아무 것도 하지 않습니다. (내부는 좀 더 복잡한 수식들로 구성되어 있지만, 이 글에서는 생략하고 넘어가도록 하겠습니다.) 이런 구조가 한층, 한층 반복되며 연결되어 있습니다. 전체를 함께 보면 복잡해 보이지만 일부만 따로 떼서 본다면, 1번째 동그라미 x 0.1 + 2번째 동그라미 x 0.2 + 3번째 동그라미 x 0.5 와 같은 형태로 표현이 가능하게 됩니다. 이 구조가 의미하는 바는 무엇일까요? 뉴럴 네트워크에 존재하는 선들의 값이 어떤 수식을 구성하는 데에 사용된다는 것입니다. 선들의 값을 바꾸면, 뉴럴 네트워크가 표현하는 수식 또한 바뀌게 됩니다.  뉴럴 네트워크 학습의 핵심은 선들의 값을 잘 찾아내는 것 올바른 선들의 값을 찾아낸다면, 연관관계를 잘 표현하는 수식을 만들어 낼 수 있게 되고, 결국 연관관계를 잘 기억해내는 잘 학습된 뉴럴 네트워크가 완성되는 것입니다. 그런데, 선들의 값을 찾는 것은 어려운 문제입니다. 최신 뉴럴 네트워크들은 수천만개, 많게는 수천억개 이상을 가지고 있습니다....