개요
(해당 글은 초기 버전에 대한 것이고 다른 글에 새 버전으로 업데이트하였습니다.)
이번 글에서는 앞서 cartpole에 대해 만들었던 Muesli 알고리즘을 LunarLander에 적용해보는 과정에서 시도해보고 있는 것들에 대해 설명하려 합니다.
앞서 LunarLander의 state, action, reward 구조에 대해 간략한 설명을 하겠습니다. LunarLander는 달에 착륙하려는 우주선이 최대한 빠르고 비용을 적게 써서 두 깃발 사이에 천천히 안착하게끔 하는 environment 입니다. State(observation)는 8-dim으로 우주선의 위치, 속도, 각도 등을 나타내며, action은 4dim으로 0: 아무것도 하지 않음, 1: 좌회전, 2: 메인엔진, 3: 우회전에 할당되어 있습니다. Reward는 내려가는 것 자체에 약간의 reward를 주고 바닥 근처까지 가면 100에서 140정도의 reward가 쌓이는데, 이는 제대로 착륙하지 않으면 없어지는 reward입니다. 그리고 crash가 일어나면 -100, 다리가 바닥에 닿으면 +10, 제대로 착륙하면 +100을 줍니다. 엔진 사용 비용은 메인엔진이 -0.3, 사이드 엔진이 -0.03을 씁니다.
이러한 구조라 cartpole보다 복잡하고 정교한 동작을 요구하는 것을 알 수 있습니다.
이를 해결하기 위해서 CartPole버전으로부터 몇가지 변화를 시도해보았습니다. 첫번째로는 hidden state를 [0,1]사이로 스케일 조정을 해줍니다. 이는 뮤제로 논문에서 소개된 내용입니다. x = (x - x.min())/(x.max() - x.min())을 representation network 및 dynamics network hs출력에 적용을 해주었습니다. 원래 hs활성화값이 상당히 크게 찍혔는데 이렇게 범위를 조정해주니 학습이 약간 개선되고 NaN 오류도 뜨지 않았습니다.
두번째는 cartpole에서 reward가 1,0으로 구성되었던 것과는 달리 100 단위의 reward가 들어가기 때문에 네트워크에 변동이 큰 것을 확인했고, reward를 일정 값으로 (/100) 나누는 시도를 했습니다. 이는 어느정도 도움이 되기는 했으나 여전히 +100 reward가 들어올 때 네트워크가 크게 흔들리는 모습을 보입니다. 이는 reward scale에 대응할 수 있게끔 advantage normalize하는 부분을 구현하거나 reward, value쪽에서 값을 regression형태로 학습하는 것이 아니라 categorical한 representation으로 학습하게끔 구조를 짜야 할 듯 합니다. Categorical representation 내용도 뮤제로 논문에도 소개되어 있습니다.
세번째는 action입력 또한 one-hot으로 바꾸어 주었습니다. CartPole은 0,1이라 문제가 없었지만 여기는 0,1,2,3이므로 이에 맞게 해주는 것이 보다 나을 듯 합니다.
네번째는 reward head랑 value head 네트워크를 약간 더 깊게 쌓아보는 시도를 했습니다.
다섯번째는 reward loss를 1/4로 나눠주었습니다.
여섯번째는 replay window를 적용해 봤습니다. 이는 episode가 길어질수록 변동폭이 작아지는 부분을 해소해주는데 학습상 유리한 것인지는 잘 모르겠습니다.
일곱번째는 hidden state를 //2로 줄여 처리했던걸 다시 늘려 사용해 봤습니다.
여덟번째는 gamma를 0.99보다 큰 값으로 변경해보았습니다.
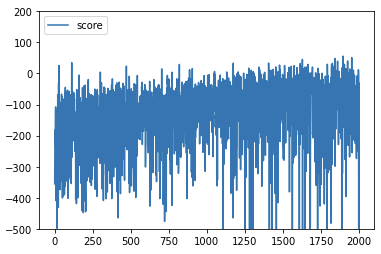
여러가지 시도를 통해서 어느정도 성능의 증가가 보이고 우주선이 전략적으로 움직이려는 모습을 보이는 상태까지는 만들었지만 score 0 근처에서 학습이 원활하게 진행되지 않고 네트워크가 흔들리는 모습을 보입니다. 여러모로 추가해야할 구현도 마저 하고 모델을 더 정교하게 짜는 시도를 추가적으로 해야겠습니다.
잘 나온 경우
##########################
##Representation Network
##input : raw input
##output : hs(hidden state)
class Representation(nn.Module):
def __init__(self, input_dim, output_dim, width):
super().__init__()
self.layer1 = torch.nn.Linear(input_dim, width)
self.layer2 = torch.nn.Linear(width, width)
self.add = torch.nn.Linear(width, width)
self.layer3 = torch.nn.Linear(width, output_dim)
def forward(self, x):
x = self.layer1(x)
x = torch.nn.functional.relu(x)
x = self.layer2(x)
x = torch.nn.functional.relu(x)
x = self.add(x)
x = torch.nn.functional.relu(x)
x = self.layer3(x)
x = (x - x.min())/(x.max() - x.min())
return x
#######################
##Dynamics Network
##input : hs, action
##output : next_hs, reward
class Dynamics(nn.Module):
def __init__(self, input_dim, output_dim, width, action_space):
super().__init__()
self.layer1 = torch.nn.Linear(input_dim + action_space, width)
self.layer2 = torch.nn.Linear(width, width)
self.hs_head = torch.nn.Linear(width, output_dim) #hidden state dim
self.reward_head = nn.Sequential(
nn.Linear(width, width),
nn.ReLU(width),
nn.Linear(width, width),
nn.ReLU(width),
nn.Linear(width, 1)
)
self.one_hot_act = F.one_hot(torch.arange(0, action_space) % action_space, num_classes=action_space)
def forward(self, x, action):
action = self.one_hot_act[action]
x = torch.cat((x,action), dim=0)
x = self.layer1(x)
x = torch.nn.functional.relu(x)
x = self.layer2(x)
x = torch.nn.functional.relu(x)
hs = self.hs_head(x)
hs = (hs - hs.min())/(hs.max() - hs.min())
reward = self.reward_head(x) # categorical representation recommended
return hs, reward
######################
##Prediction Network
##input : hs
##output : P, V
class Prediction(nn.Module):
def __init__(self, input_dim, output_dim, width):
super().__init__()
self.layer1 = torch.nn.Linear(input_dim, width)
self.layer2 = torch.nn.Linear(width, width)
self.policy_head = torch.nn.Linear(width, output_dim) #action space dim
self.value_head = nn.Sequential(
nn.Linear(width, width),
nn.ReLU(width),
nn.Linear(width, width),
nn.ReLU(width),
nn.Linear(width, 1)
)
def forward(self, x):
x = self.layer1(x)
x = torch.nn.functional.relu(x)
x = self.layer2(x)
x = torch.nn.functional.relu(x)
P = self.policy_head(x)
P = torch.nn.functional.softmax(P, dim=0)
V = self.value_head(x) # categorical representation recommended
return P, V







댓글
댓글 쓰기