개요
(해당 글은 초기 버전에 대한 것이고 다른 글에 새 버전으로 업데이트하였습니다.)
Muesli(뮤즐리) 알고리즘을 PyTorch 코드로 구현하였으며 Colab에서 코드 실행 및 결과 확인이 가능합니다. 이번 글에서는 구현한 뮤즐리 코드와 함께 설명하려 합니다.
설명
(전체 코드는 위의 Colab링크 및 이전 글에 있습니다.)
먼저 뮤즐리 구현에 사용된 뮤제로 네트워크 구조에 대해 설명합니다.
##Muesli agent
class Agent(nn.Module):
def __init__(self, state_dim, action_dim, width, target=0):
super().__init__()
self.representation_network = Representation(state_dim, state_dim//2, width)
self.dynamics_network = Dynamics(state_dim//2, state_dim//2, width)
self.prediction_network = Prediction(state_dim//2, action_dim, width)
self.optimizer = torch.optim.AdamW(self.parameters(), lr=0.0003, weight_decay=0)
#self.scheduler = torch.optim.lr_scheduler.ExponentialLR(self.optimizer, gamma=0.999)
self.to(device)
self.train()
self.state_traj = []
self.action_traj = []
self.P_traj = []
self.r_traj = []
self.state_replay = []
self.action_replay = []
self.P_replay = []
self.r_replay = []
self.action_space = action_dim
self.env = gym.make(game_name)
######################
##Representation Network
##input : raw input
##output : hs(hidden state)
class Representation(nn.Module):
def __init__(self, input_dim, output_dim, width):
super().__init__()
self.layer1 = torch.nn.Linear(input_dim, width)
self.layer2 = torch.nn.Linear(width, width)
self.layer3 = torch.nn.Linear(width, output_dim)
def forward(self, x):
x = self.layer1(x)
x = torch.nn.functional.relu(x)
x = self.layer2(x)
x = torch.nn.functional.relu(x)
x = self.layer3(x)
return x
연산시 가장 먼저 inference되는 네트워크인 representation network는 raw input(observation)을 hidden state로 바꿔주는 네트워크입니다. 구현에서는 간단한 mlp를 사용했습니다. Cartpole환경은 state dim이 4이므로 충분하게 사용이 가능합니다. (뉴런수는 128개를 사용하였습니다). Hidden state는 raw input의 대략 절반의 크기인 2로 관리가 되게끔 했습니다.
######################
##Prediction Network
##input : hs
##output : P, V
class Prediction(nn.Module):
def __init__(self, input_dim, output_dim, width):
super().__init__()
self.layer1 = torch.nn.Linear(input_dim, width)
self.layer2 = torch.nn.Linear(width, width)
self.policy_head = torch.nn.Linear(width, output_dim)
self.value_head = torch.nn.Linear(width, 1)
def forward(self, x):
x = self.layer1(x)
x = torch.nn.functional.relu(x)
x = self.layer2(x)
x = torch.nn.functional.relu(x)
P = self.policy_head(x)
P = torch.nn.functional.softmax(P, dim=0)
V = self.value_head(x)
return P, V
Prediction network는 hidden state로부터 policy및 value inference를 담당하는 네트워크입니다. 네트워크 중간에 각각에 대한 head를 통해 출력하는 구조입니다. Policy 출력은 action space dim과 동일한 사이즈이며 softmax 처리되어 출력됩니다.
######################
##Dynamics Network
##input : hs, action
##output : next_hs, reward
class Dynamics(nn.Module):
def __init__(self, input_dim, output_dim, width):
super().__init__()
self.layer1 = torch.nn.Linear(input_dim + 1, width)
self.layer2 = torch.nn.Linear(width, width)
self.hs_head = torch.nn.Linear(width, output_dim)
self.reward_head = torch.nn.Linear(width, 1)
def forward(self, x, action):
action = torch.tensor([action])
x = torch.cat((x,action), dim=0)
x = self.layer1(x)
x = torch.nn.functional.relu(x)
x = self.layer2(x)
x = torch.nn.functional.relu(x)
hs = self.hs_head(x)
reward = self.reward_head(x)
return hs, reward
Dynamics network는 hidden state의 state transition을 지원하고 reward inference를 가능하게 하는 네트워크입니다. hs를 다음 hs로 transition해주고 reward head를 통해서 reward inference를 합니다. (이 네트워크는 unroll시 네트워크의 허리의 역할을 하기 때문인지 뮤제로 논문에 소개된대로 역전파시에 gradient를 1/2로 해주는 것이 학습 안정성에 꽤나 큰 영향을 줍니다.)
아래 그림은 위에서의 네트워크들을 사용해 unroll할때의 연산 흐름입니다. h가 representation, g가 dynamics, f가 prediction network입니다.
아래 코드는 main역할을 하는 부분으로 초기화 및 self-play, training하는 loop부분을 나타냅니다.
device = torch.device('cpu')
score_arr = []
game_name = 'CartPole-v1'
env = gym.make(game_name)
target = Target(env.observation_space.shape[0], env.action_space.n, 128)
agent = Agent(env.observation_space.shape[0], env.action_space.n, 128)
print(agent)
env.close()
target.load_state_dict(agent.state_dict())
#Self play, weight update
episode_nums = 1000
for i in range(episode_nums):
if i%30==0:
params1 = agent.named_parameters()
params2 = target.named_parameters()
dict_params2 = dict(params2)
for name1, param1 in params1:
if name1 in dict_params2:
dict_params2[name1].data.copy_(0.5*param1.data + 0.5*dict_params2[name1].data)
target.load_state_dict(dict_params2)
game_score = agent.self_play_mu()
score_arr.append(game_score)
if i%10==0:
print('episode', i)
print('score', game_score)
t_game_score = agent.target_performence_test(target)
print('t_score', t_game_score)
if np.mean(np.array(score_arr[i-5:i])) > 400:
torch.save(agent.state_dict(), 'weights.pt')
break
agent.update_weights_mu(target)
torch.save(agent.state_dict(), 'weights.pt')
agent.env.close()
게임 env설정 및 agent, target network를 초기화 해주고, target network가 agent파라미터와 동일하게 해주고, self-play와 training을 반복합니다. Loop내의 if i%30==0: 부분은 논문에 있는 내용은 아닌데 구현상 target network와 update하는 네트워크의 거리가 너무 멀어지지 않게 적당한 시점마다 target network가 따라오게끔 하는 목적으로 추가한 부분입니다.
아래 코드는 self play하는 부분으로 representation network로 hs 만들고 이를 prediction network가 policy inference하고 이에 따라 action을 취하고 데이터를 모아 저장합니다. 논문의 pseudocode에서는 target network를 따라서 self play를 진행하는데, 그렇게 해도 학습이 진행되기는 합니다만 제 구현에서는 학습속도가 느린 부분이 있어서 업데이트된 네트워크를 가지고 self play를 하게끔 했습니다.
def self_play_mu(self, max_timestep=10000):
#self play with 1st inferenced policy
game_score = 0
state = self.env.reset()
for i in range(max_timestep):
start_state = state
with torch.no_grad():
hs = self.representation_network(torch.from_numpy(state).float().to(device))
P, v = self.prediction_network(hs)
action = np.random.choice(np.arange(self.action_space), p=P.detach().numpy())
state, r, done, _ = self.env.step(action)
self.state_traj.append(start_state)
self.action_traj.append(action)
self.P_traj.append(P)
self.r_traj.append(r)
game_score += r
if done:
break
# for update inference over trajectory length
self.state_traj.append(np.zeros_like(state))
self.state_traj.append(np.zeros_like(state))
self.r_traj.append(torch.tensor(0))
self.action_traj.append(np.random.randint(self.action_space))
# traj append to replay
self.state_replay.append(self.state_traj)
self.action_replay.append(self.action_traj)
self.P_replay.append(self.P_traj)
self.r_replay.append(self.r_traj)
return game_score
아래는 앞선 글에서 설명한 학습 알고리즘 부분이 구현된 부분입니다. 먼저 이 부분 코드 전체를 첨부하고 아래에서 부분별로 설명하도록 하겠습니다.
def update_weights_mu(self, target):
for _ in range(20): ## number of minibatch
Cumul_L_total = 0
for epi_sel in range(6): ## number of selected episode in a batch
if(epi_sel>0):## replay proportion
sel = np.random.randint(0,len(self.state_replay))
self.state_traj = self.state_replay[sel]
self.action_traj = self.action_replay[sel]
self.P_traj = self.P_replay[sel]
self.r_traj = self.r_replay[sel]
## multi step return G (orignally retrace used)
G = 0
G_arr = []
for r in self.r_traj[::-1]:
G = 0.99 * G + r
G_arr.append(G)
G_arr.reverse()
G_arr.append(torch.tensor(0))
G_arr.append(torch.tensor(0))
for i in np.random.randint(len(self.state_traj)-2,size=5): ## number of selected transition in a replay
## update inference (2 step unroll. originally 5 step unroll recommended)
first_hs = self.representation_network(torch.from_numpy(self.state_traj[i]).float().to(device))## do not have to stack more than 1 frame
first_P, first_v = self.prediction_network(first_hs)
second_hs, r = self.dynamics_network(first_hs, self.action_traj[i])
second_P, second_v = self.prediction_network(second_hs)
third_hs, r2 = self.dynamics_network(second_hs, self.action_traj[i+1])
third_P, third_v = self.prediction_network(third_hs)
## target network inference
with torch.no_grad():
t_first_hs = target.representation_network(torch.from_numpy(self.state_traj[i]).float().to(device))
t_first_P, t_first_v = target.prediction_network(t_first_hs)
## L_pg_cmpo first term (eq.10)
importance_weight = torch.clip(first_P.gather(0,torch.tensor(self.action_traj[i]))
/(self.P_traj[i].gather(0,torch.tensor(self.action_traj[i])).item()),
0, 1
)
first_term = -1 * importance_weight * (G_arr[i].item() - t_first_v.item())
##lookahead inferences (one step look-ahead to some actions to estimate q_prior, from target network)
with torch.no_grad():
r1_arr = []
v1_arr = []
a1_arr = []
for _ in range(self.action_space): #sample <= N(action space), now N
action1 = np.random.choice(np.arange(self.action_space), p=t_first_P.detach().numpy())#prior pi
hs, r1 = target.dynamics_network(t_first_hs, action1)
_, v1 = target.prediction_network(hs)
r1_arr.append(r1)
v1_arr.append(v1)
a1_arr.append(action1)
## z_cmpo_arr (eq.12)
with torch.no_grad():
adv_arr = []
for r1, v1 in zip(r1_arr, v1_arr):
adv = r1 + 0.99 * v1 - t_first_v # adv = q_prior - v_prior. q_prior = r1 + gamma* v1
adv_arr.append(adv)
exp_clip_adv_arr = [torch.exp(torch.clip(adv_arr[k], -1, 1)) for k in range(self.action_space)]
z_cmpo_arr = []
for k in range(self.action_space):
z_cmpo = (1 + torch.sum(torch.tensor(exp_clip_adv_arr)) - exp_clip_adv_arr[k]) / self.action_space
z_cmpo_arr.append(z_cmpo)
## L_pg_cmpo second term (eq.11)
second_term = 0
for k in range(self.action_space):
second_term += exp_clip_adv_arr[k]/z_cmpo_arr[k] * torch.log(first_P.gather(0, torch.tensor(a1_arr[k])))
regularizer_multiplier = 5
second_term *= -1 * regularizer_multiplier / self.action_space
## L_pg_cmpo
L_pg_cmpo = first_term + second_term
## L_v
L_v = (
((first_v - G_arr[i].item())**2)/2
+ ((second_v - G_arr[i+1].item())**2)/2
+ ((third_v - G_arr[i+2].item())**2)/2
)
## L_r
L_r = ((r - self.r_traj[i])**2)/2 + ((r2-self.r_traj[i+1])**2)/2
## L_m (eq 7, eq 13)
L_m = 0
m_adv_arr = []
with torch.no_grad():
m_hs = target.representation_network(torch.from_numpy(self.state_traj[i+1]).float().to(device))
m_P, m_v = target.prediction_network(m_hs)
for j in range(self.action_space):
hs, r = target.dynamics_network(m_hs, j)
_, v = target.prediction_network(hs)
m_adv = r + 0.99 * v - m_v
m_adv_arr.append(torch.exp(torch.clip(m_adv,-1,1)))
pi_cmpo_all = [m_P[j]*m_adv_arr[j]/(1+sum(m_adv_arr)-m_adv_arr[j])*self.action_space for j in range(self.action_space)]
pi_cmpo_all=torch.tensor(pi_cmpo_all)
kl_loss = torch.nn.KLDivLoss()
L_m += kl_loss(F.log_softmax(second_P, dim=0), F.softmax(pi_cmpo_all,dim=0))#input, target
m_adv_arr = []
with torch.no_grad():
m_hs = target.representation_network(torch.from_numpy(self.state_traj[i+2]).float().to(device))
m_P, m_v = target.prediction_network(m_hs)
for j in range(self.action_space):
hs, r = target.dynamics_network(m_hs, j)
_, v = target.prediction_network(hs)
m_adv = r + 0.99 * v - m_v
m_adv_arr.append(torch.exp(torch.clip(m_adv,-1,1)))
pi_cmpo_all = [m_P[j]*m_adv_arr[j]/(1+sum(m_adv_arr)-m_adv_arr[j])*self.action_space for j in range(self.action_space)]
pi_cmpo_all=torch.tensor(pi_cmpo_all)
kl_loss = torch.nn.KLDivLoss()
L_m += kl_loss(F.log_softmax(third_P, dim=0) , F.softmax(pi_cmpo_all,dim=0))
L_m /= 2
L_total = L_pg_cmpo + L_v/3/4 + L_r/2 + L_m/4
Cumul_L_total += L_total
Cumul_L_total /= 30
self.optimizer.zero_grad()
Cumul_L_total.backward()
nn.utils.clip_grad_value_(self.parameters(), clip_value=1.0)
## dynamics network gradient scale 1/2
for d in self.dynamics_network.parameters():
d.grad *= 0.5
self.optimizer.step()
## target network(prior parameters) moving average update
alpha_target = 0.01
params1 = self.named_parameters()
params2 = target.named_parameters()
dict_params2 = dict(params2)
for name1, param1 in params1:
if name1 in dict_params2:
dict_params2[name1].data.copy_(alpha_target*param1.data + (1-alpha_target)*dict_params2[name1].data)
target.load_state_dict(dict_params2)
#self.scheduler.step()
##trajectory clear
self.state_traj.clear()
self.action_traj.clear()
self.P_traj.clear()
self.r_traj.clear()
return
[부분 1]
def update_weights_mu(self, target):
for _ in range(20): ## number of minibatch
Cumul_L_total = 0
for epi_sel in range(6): ## number of selected episode in a batch
if(epi_sel>0):## replay proportion
sel = np.random.randint(0,len(self.state_replay))
self.state_traj = self.state_replay[sel]
self.action_traj = self.action_replay[sel]
self.P_traj = self.P_replay[sel]
self.r_traj = self.r_replay[sel]
## multi step return G (orignally retrace used)
G = 0
G_arr = []
for r in self.r_traj[::-1]:
G = 0.99 * G + r
G_arr.append(G)
G_arr.reverse()
G_arr.append(torch.tensor(0))
G_arr.append(torch.tensor(0))
for i in np.random.randint(len(self.state_traj)-2,size=5): ## number of selected transition in a replay
미니배치 업데이트를 하기 위해서 몇개의 for루프가 겹쳐져 있는 형태이고, 그 중간에는 replay buffer로부터 배치를 구성할 transition들을 랜덤하게 뽑아올 수 있게 하는 코드가 들어 있습니다. 깔끔하게 데이터를 묶어서 배치로 구성해서 GPU로 던져줄 수 있게 하는 코드가 바람직하겠지만 지금 코드는 한 transition마다 따로 gradient구해서 accumulate해서 나누는 식으로 구성이 되어 있습니다. (학습속도는 느리지만 알고리즘 들여다보기엔 비교적 직관적인 장점이 있습니다. 추후에 GPU버전으로 만드려 합니다.)
가져온 replay buffer로부터 가져온 trajectory로부터 multi step return G를 구하는 부분도 포함되어 있습니다. 저는 reward로부터 단순하게 구하는 방법을 썻지만 논문의 알고리즘에서는 이를 Retrace estimator로 보다 정교하게 구합니다. Retrace는 모델로부터 reward, value를 구한 것에 기반해 구성한 q값을 사용하여 importance sampling을 하면서 보다 정교한 return을 구합니다. 이는 뮤즐리의 성능에 상당히 큰 차이를 줍니다(거의 2배). 다만 저는 아직 이해가 부족해서 생략하였습니다.
[부분 2]
## update inference (2 step unroll. originally 5 step unroll recommended)
first_hs = self.representation_network(torch.from_numpy(self.state_traj[i]).float().to(device))## do not have to stack more than 1 frame
first_P, first_v = self.prediction_network(first_hs)
second_hs, r = self.dynamics_network(first_hs, self.action_traj[i])
second_P, second_v = self.prediction_network(second_hs)
third_hs, r2 = self.dynamics_network(second_hs, self.action_traj[i+1])
third_P, third_v = self.prediction_network(third_hs)
## target network inference
with torch.no_grad():
t_first_hs = target.representation_network(torch.from_numpy(self.state_traj[i]).float().to(device))
t_first_P, t_first_v = target.prediction_network(t_first_hs)
해당 부분은 update할 네트워크를 unroll하는 부분입니다. 그리고 계산과정에서 target network의 값도 필요한 부분이 있어서 한단계 inference를 합니다. Target network는 직접 학습되지는 않습니다.
[부분 3]
## L_pg_cmpo first term (eq.10)
importance_weight = torch.clip(first_P.gather(0,torch.tensor(self.action_traj[i]))
/(self.P_traj[i].gather(0,torch.tensor(self.action_traj[i])).item()),
0, 1
)
first_term = -1 * importance_weight * (G_arr[i].item() - t_first_v.item())
10번 식의 구현입니다. (식 설명은 앞글에 있습니다.). Unroll한 policy인 first_P, behavior policy인 P_traj로 구성을 하고 논문에 써진 대로 [0,1]로 clip해줍니다. G는 위에서 구했던 multi step return값을 써주고, v는 target network(prior)로부터 inference한 값을 써줍니다.
[부분 4]
##lookahead inferences (one step look-ahead to some actions to estimate q_prior, from target network)
with torch.no_grad():
r1_arr = []
v1_arr = []
a1_arr = []
for _ in range(self.action_space): #sample <= N(action space), now N
action1 = np.random.choice(np.arange(self.action_space), p=t_first_P.detach().numpy())#prior pi
hs, r1 = target.dynamics_network(t_first_hs, action1)
_, v1 = target.prediction_network(hs)
r1_arr.append(r1)
v1_arr.append(v1)
a1_arr.append(action1)
## z_cmpo_arr (eq.12)
with torch.no_grad():
adv_arr = []
for r1, v1 in zip(r1_arr, v1_arr):
adv = r1 + 0.99 * v1 - t_first_v # adv = q_prior - v_prior. q_prior = r1 + gamma* v1
adv_arr.append(adv)
exp_clip_adv_arr = [torch.exp(torch.clip(adv_arr[k], -1, 1)) for k in range(self.action_space)]
z_cmpo_arr = []
for k in range(self.action_space):
z_cmpo = (1 + torch.sum(torch.tensor(exp_clip_adv_arr)) - exp_clip_adv_arr[k]) / self.action_space
z_cmpo_arr.append(z_cmpo)
## L_pg_cmpo second term (eq.11)
second_term = 0
for k in range(self.action_space):
second_term += exp_clip_adv_arr[k]/z_cmpo_arr[k] * torch.log(first_P.gather(0, torch.tensor(a1_arr[k])))
regularizer_multiplier = 5
second_term *= -1 * regularizer_multiplier / self.action_space
## L_pg_cmpo
L_pg_cmpo = first_term + second_term
이렇게 위에서 구한 first term과 second term을 합쳐서 식 9를 구성을 해 줍니다.
[부분 5]
[부분 5]
## L_v
L_v = (
((first_v - G_arr[i].item())**2)/2
+ ((second_v - G_arr[i+1].item())**2)/2
+ ((third_v - G_arr[i+2].item())**2)/2
)
## L_r
L_r = ((r - self.r_traj[i])**2)/2 + ((r2-self.r_traj[i+1])**2)/2
value model과 reward model(prediction network의 value head랑 dynamics network의 reward head)부분을 학습시켜주기 위해서 위에서 unroll했던 네트워크와 trajectory에서 계산한 값으로 loss를 구성해줍니다.
[부분 6]
## L_m (eq 7, eq 13)
L_m = 0
m_adv_arr = []
with torch.no_grad():
m_hs = target.representation_network(torch.from_numpy(self.state_traj[i+1]).float().to(device))
m_P, m_v = target.prediction_network(m_hs)
for j in range(self.action_space):
hs, r = target.dynamics_network(m_hs, j)
_, v = target.prediction_network(hs)
m_adv = r + 0.99 * v - m_v
m_adv_arr.append(torch.exp(torch.clip(m_adv,-1,1)))
pi_cmpo_all = [m_P[j]*m_adv_arr[j]/(1+sum(m_adv_arr)-m_adv_arr[j])*self.action_space for j in range(self.action_space)]
pi_cmpo_all=torch.tensor(pi_cmpo_all)
kl_loss = torch.nn.KLDivLoss()
L_m += kl_loss(F.log_softmax(second_P, dim=0), F.softmax(pi_cmpo_all,dim=0))#input, target
m_adv_arr = []
with torch.no_grad():
m_hs = target.representation_network(torch.from_numpy(self.state_traj[i+2]).float().to(device))
m_P, m_v = target.prediction_network(m_hs)
for j in range(self.action_space):
hs, r = target.dynamics_network(m_hs, j)
_, v = target.prediction_network(hs)
m_adv = r + 0.99 * v - m_v
m_adv_arr.append(torch.exp(torch.clip(m_adv,-1,1)))
pi_cmpo_all = [m_P[j]*m_adv_arr[j]/(1+sum(m_adv_arr)-m_adv_arr[j])*self.action_space for j in range(self.action_space)]
pi_cmpo_all=torch.tensor(pi_cmpo_all)
kl_loss = torch.nn.KLDivLoss()
L_m += kl_loss(F.log_softmax(third_P, dim=0) , F.softmax(pi_cmpo_all,dim=0))
L_m /= 2

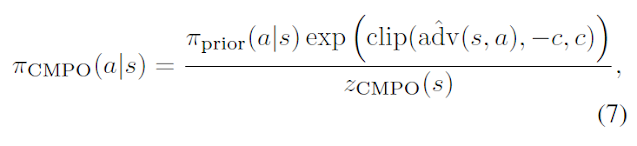
이 부분은 model loss L_m 을 구하는 부분으로 target network로부터 구한 policy_cmpo로 구성된 확률분포와 (이는 target network로부터 구하며 s_t+k(observation)로부터 새로 inference) 업데이트할 네트워크의 확률분포를 가지고 KL divergence loss로 식을 구성합니다.
글이 길어지다보니 블로그 에디터가 느려지기 시작해서 다음글에서 이어서 설명하겠습니다.











댓글
댓글 쓰기