개요
https://arxiv.org/abs/1706.03762 (Attention Is All You Need, Transformer, 트랜스포머 논문링크)
최근 몇 년 동안 자언여처리 붐이 일고 있다. 규모 있는 기업들 상당수가 고성능 자연어처리 프로그램인 거대언어모델(Large Language Model) 개발에 집중하고 있다. 구글, 페이스북, OpenAI, 네이버, 카카오, LG, KT 등 많은 기업들이 결과물들을 내놓고 있다. 많이 들어본 GPT-3가 OpenAI의 결과물 중 하나이다. 최근 들어서는 성능이 더 좋아지고 있다. 프로그램이 수학 문제를 '주관식'으로 풀어낼 수가 있는 정도이다. 링크
언어모델은 분류, 질답, 생성, 번역, 요약 등 여러 task들에 사용될 수 있는데, 이러한 task들은 대체적으로 긴 문장 뒤에 어떤 단어 혹은 문장이 나오는 동작을 한다. 이러한 동작을 가능하게 하는 기술적 기반 중 가장 많이 쓰이고 있는 것이 트랜스포머(transformer)라는 구조이다. 이번 글에서는 트랜스포머의 구조, 특성, 배경, 관련 자료 등 여러가지를 소개하려 한다.
트랜스포머 등장 배경
트랜스포머 이전의 자연어처리 모델들은 긴 문장을 차례대로 움직이면서 단어 사이의 관계나 의미를 계산하는 형태의 동작을 한다. 하지만 이렇게 순차적으로 움직이는 것은 병렬컴퓨팅을 하기에 불리한 구조이다. 아무리 컴퓨터가 좋아도 계산속도에는 한계가 있는 것이다. 트랜스포머는 기존 모델들이 하는 일들을 모두 잘 해내면서도 병렬컴퓨팅에 유리한 구조를 가진 덕분에, 모델 사이즈를 엄청나게 키우고 GPU를 수천개 이상 붙여서 자원을 쏟아붓는 만큼 자연어 처리 성능이 쭉쭉 오르는 것을 가능하게 해주었다.
병렬 처리에 유리하게 된 연산은 attention 연산(긴 문장의 단어 사이의 관계를 계산)인데, 기존은 attention 연산에 순차적인 요소가 있었다면 트랜스포머는 순차적인 부분 없이 한방에 연산을 한다. 트랜스포머 논문 저자는 논문 제목을 통해 attention의 중요성에 대해 이야기하고 있다. 논문 제목은 "Attention Is All You Need"이다. (자연어 처리를 하는 데 있어서) attention 연산 하나만 효과적으로 잘 처리할 수 있으면 다 된다는 것이다.
자세한 내용을 다루기 전에, 트랜스포머는 기본적으로 encoder-decoder 구조를 가지고 있다. 긴 문장이 있으면, 그 문장을 어떻게든 다른 표현으로 압축하고, 압축한 표현을 다시 다른 긴 문장으로 변환하는 식이다. 문장을 압축하고 압축을 푸는 과정에서 attention 연산이 사용되는 구조를 가지고 있다.
이어서 트랜스포머의 구조를 연산 흐름 순으로 설명하려 한다.
트랜스포머 구조
Inputs는 그냥 평범한 문장 데이터이다. 이 페이지에 있는 글자, 기호, 숫자, 띄어쓰기 등등이 모두 각자의 코드를 가지고 있고 그에 기반해 표현되고 있다. 근데 이 데이터를 그대로 집어넣는 것이 학습에 충분한가 하면 그렇지 않은 것 같다. 각 단어들을 적절한 token으로 나누는 단계를 거친다. 대략 이러하다. ['각' '단어' '들' '을' '적절' '한' 'token' '으로' '나누' '는' '단계' '를' '거친다' '.']. 자주 쓰이는 단어 단위로 적절하게 잘 나누면 표현에 낭비를 줄이고 자주 쓰이는 몇만개의 토큰으로 잘 정리할 수 있다고 한다. 예를 들어 적절히, 적절한, 적절하게, 적절하다 등을 하나하나를 각각 표현하느니 잘 나눠서 자주 쓰이는 부분들을 우선적으로 정리하면 효율적일 것이다. 이러한 일을 해주는 것이 tokenizer이다.
이렇게 tokenizer에 의해 적절한 token으로 나눠진 문장 데이터는 학습을 하기에 충분한가 하면 또 그렇지 않은 것 같다. 이런 token들은 정수로 표현이 되는데, 예를 들면 위에서 token화 된 문장의 표현은 [3489, 378, 4589, 3489, 278, 3580, 4905 ...] 와 같은 형태이다. 이 숫자 하나하나가 각 token들에 대해 연관은 지어주겠지만 정보 표현 측면에서는 충분하지 않다. 만약 '개' 토큰이 300이고 '고양이' 토큰이 500이면 둘이 특별한 연관이 있다고 할 수는 없다.
그래서 토큰화된 문장을 임베딩하는 과정을 거친다. Word2vec와 같은 임베딩 알고리즘이 토큰들의 관계를 분석해서 의미를 더 깊게 표현할 수 있는 형태로 토큰을 바꾼다. 각 정수 형태의 토큰들은 [0.0213 0.003 0.0211 ........... 0.3213 0.9813] 과 같은 512 dimension을 가진 벡터 형태로 표현된다. 이렇게 임베딩되면 '개' 토큰과 '고양이' 토큰은 꽤나 연관이 있을 수 있게 된다.
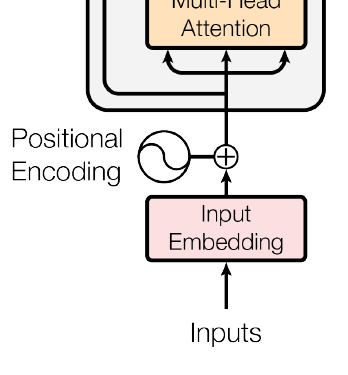
그래서 위 그림에서처럼 positional encoding을 해주어야 한다. 임베딩된 토큰 벡터들에다 위치 정보를 더해주는 것이다. 구글에 plot y=sin(2/10000^(2*x/512)) 을 검색해 보면 신기하게 생긴 파동 형태의 함수가 나타난다. 이러한 정보를 각각의 벡터들에 추가해주는 것이다. 드디어 attention연산을 할 준비가 되었다.
Self-attention 연산
512-dimension을 가진 위치정보가 들어간 임베딩된 토큰 벡터들이 길게 늘어서 있고 (이제 이 벡터들을 x 라 칭한다. [x1, x2, ... ,xn] 형태임), x 벡터들은 이제 self-attention연산에 사용된다. 각 x 벡터는 3가지의 형태로 변환되는데 각각 Query 벡터, Key 벡터, Value 벡터이다. 하나의 x 벡터마다 Query 벡터, Key 벡터, Value 벡터 각각 하나씩 도출된다. 계산은 x와 Query weight matrix, x와 Key weight matrix, x와 Value weight matrix 각각 행렬곱을 함으로서 진행된다. (논문에서는 linearly project한다는 표현을 사용한다.)
(이렇게 도출된 Query 벡터, Key 벡터, Value 벡터는 weight matrix들이 충분히 학습되기 전에는 별다른 의미를 가지지는 못할 것이다. 하지만 학습 과정에서 weight matrix들이 적절한 파라미터를 찾게 된다면 힘을 발휘할 가능성이 있는 것이다.)
이제 [x1, x2, ... xn] 은 [(q1,k1,v1), (q2,k2,v2), ....,(qn,kn,vn)] 형태로 바뀌었다. 이제 여기서 본격적으로 attention 메커니즘이 활용된다. Attention 메커니즘은 긴 문장의 토큰들 사이의 관계를 계산하는 동작을 하는데 만약 x1은 x1, x2, ... xn와 어떤 관계가 있을까? x2는 x1, x2, ... xn와 어떤 관계가 있을까? x3은, x4는, ... , xn은? 을 모두 계산하는 구조를 가지고 있다.
설명에 앞서 Query 벡터, Key 벡터, Value 벡터에 대한 설명을 간략하게 하고 넘어간다. 먼저 Value 벡터 v는 x의 본질적인 정보를 내포하고 있다. 예를 들어 x가 사과이면 Value 벡터 v는 사과 그 자체에 대한 표현을 담고 있을 것이다. 그리고 사과는 여러가지 고유한 특징을 가지고 있을 것인데(예를 들면 빨갛고 둥근 특성) 이런 특징 정보를 Key 벡터 k가 담아줄 수 있다. 수동적으로 집중을 끌어올 수 있는 정보들인 것이다.
Query 벡터 q는 다른 key들과 연관지어질 수 있는 가능성을 만들어주는, 보다 능동적으로 외부에 집중하고자 하는 벡터이다. 빨갛고 둥근 특성을 가지고 있다고 해서 꼭 빨갛고 둥근 무언가를 찾아 연관지을 필요는 없을 것이다. 다른 차원의 특성을 연관지을 수 있는 것이 좋을 것이다. 갯수라던지, 동사, 지시대명사와 같은 것에도 적절한 관심을 가져야 할 것이다. (꼭 위에서 설명한것과 같이 key와 query가 가지는 내용이 명시적으로 지시되는것은 아닐테지만 의미상 그러한 동작을 하지 않을까 해서 위와 같이 비유하였습니다. 위 두 문단은 본인만의 해석(뇌피셜)이니 참고 부탁드립니다)
먼저 x1의 경우인 'x1은 x1, x2, ... xn와 어떤 관계가 있을까?' 의 경우만 따로 떼서 연산과정을 설명한다. (본래 attention연산은 x1~xn 모두의 연산을 한번에 엮어 계산한다. 이는 이후 문단에서 설명한다.) 연산에는 위에서 구했던 [(q1,k1,v1), (q2,k2,v2), ....,(qn,kn,vn)]가 사용된다.
q1을 k1,k2,k3~,kn 각각과 dot product 해서 얼마나 연관이 있는지를 나타내는 attention score 벡터를 구한다. 그리고 이 벡터를 softmax처리를 한번 한다. 그 결과로 나오는 벡터의 원소 하나하나는 x1이 x1,x2,x3~,kn 각각과 얼만큼 연관성이 있는지에 대한 정보를 가지고 있을 것이다. 그 원소 하나하나가 알려주는 연관 강도만큼 v1,v2,v3~,vn에 각각 가중(곱)한다. 그리고 그렇게 가중된 v 벡터들을 전부 더한다. 최종적으로 합해진 벡터는 x1이 x1, x2, ... xn 와 어떤 연관성을 가지고 있는지에 대한 정보를 함축하고 있는 attention value 벡터가 된다.
이렇게 x1에 대한 attention value 벡터를 구한 것이 의미하는 바는 무엇일까? 만약 x1이 사과이면 attention 연산 전에 x1은 그저 '사과'였을 뿐이다. 하지만 attention연산의 힘으로 '사과' 에서 '맛있는 빨간 사과 5개' 와 같은 표현력이 더 좋은 정보로 변하게 되는 것이다.
위에서는 x1에 대해서만 계산했지만, 나머지 x2, x3, ... , xn 모두에 대해서도 각각의 attention value 벡터를 구해야 할 것이다.
실제 연산 과정에서는 위의 설명처럼 한 x 벡터마다 위와 같은 연산을 하지 않는다. 행렬곱을 사용해 전부 한번에 계산하는 형태이다. 그러기 위해 먼저 q벡터들을 쌓아서 Q 행렬로 만든다. k벡터들을 쌓아 K행렬로 만들고 이를 transpose한다. 그리고 Q와 transpose된 K를 행렬곱한다. 결과로 나온 행렬은 각 x들에서 구한 attention score벡터들을 쌓은 것과 같다. 그리고 attention score벡터의 각 행마다 softmax처리를 하게 한다. 그렇게 나온 softmax & scaled된 attention score 행렬과, v벡터들을 쌓은 V행렬을 행렬곱한다. 이 결과로 나온 행렬은 각 x들에서 구한 attention value 벡터들을 쌓은 것과 같다. 최종적으로 n개의 attention value 벡터가 쌓여있는 형태의 행렬이 나왔고 이는 한번의 attention 연산의 최종 결과가 된다.
그림에서 Attention 연산을 하는 부분
Attention 연산 식.
(식에서 dk(q,k의 표현 dimension)의 root로 나누는 부분은 학습을 원활하게 하기 위해 scale 조정을 하는 부분이다.)
행렬 연산흐름
위에서 구한 attention value 행렬은 바로 다음 연산으로 들어가지는 않는다. Multi-head attention이라는 방법이 쓰이는데, 큰 화면을 가진 TV하나로 보는 것 대신, 작은 모니터 8개를 통해 보는 것과 비슷하다고 볼 수 있다. (여기서도 한번 linearly project 된다.) 자세한 부분은 흐름상 생략한다.
Multi-head attention의 결과값은 residual하게 연결되고 layer normalize된다(Add & Norm). (두 동작 모두 모델이 deep해지는 경우에 학습의 용이함을 위한 최적화 기법이다.) 그리고 Position-wise하게 계산하는 2개의 레이어를 가진 Feed-Forward Networks에 통과된다. 이에 대한 자세한 설명은 흐름상 생략한다. 이후 여기 또한 residual하게 연결되고 layer normalize된다. 이렇게 한 encoding layer의 동작이 끝난다.
이렇게 인코딩된 정보를 바탕으로 그 다음에 올 단어를 예측하는 과정인 디코딩 과정을 진행해야 한다. 전체 그림에서 오른쪽 부분이다. 다음 글에서 추가로 설명하려고 한다.
댓글
댓글 쓰기